符号解释
(x,y):其中x表示一个nx维度的数据,为输入数据,维度为(nx,1),也是一个nx维的特征向量,y表示标签
用大写X表示训练集矩阵,X是一个规模为nx乘以m的矩阵,X.shape()会返回(nx,m),由m个样例组成的训练集矩阵,第一个样例放在第一列……。而训练集的输入标签Y也可以用一个(1,m)的矩阵表示。
上标圆括号(i)表示第i个训练样本。
原理
逻辑回归定义的损失函数不再是差的平方的一半,原因是当学习权重参数的时候,会发现如果用差的平方和,优化目标不是凸优化(代价函数不是凸函数),只能找到多个局部最小,GD算法可能找不到全局最优。
所以,这里我们定义的损失函数是:
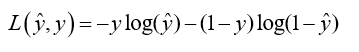
损失函数是对单个训练样本定义的,它衡量的是单个训练样本在算法中表现如何,为了衡量在训练集算法效果,引入代价函数,是对m个样本的损失函数求和除以m。
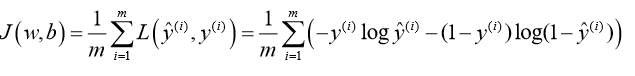
训练的时候对代价函数GD算法即可。
梯度下降
3.1 单个样本损失函数:
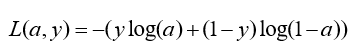
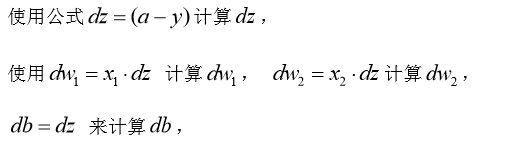
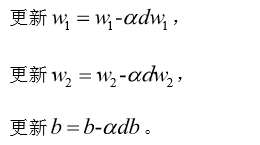
3.2 m个样本的梯度下降
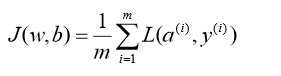
使用一个for循环遍历训练集。同时,计算相应的每个训练样本的微分,然后将他们加起来。让i从1取到m,m正好是训练样本的个数。


上述方法:有两个for循环,第一个是循环遍历m个样本,第二个是循环遍历所有特征(上面例子只有两个特征w1,w2,nx=2)。可以采用向量化加速运算。
向量化
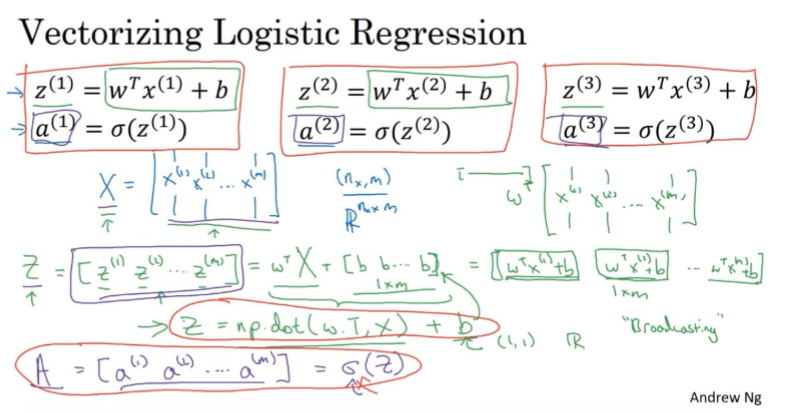

内层j的循环去掉,向量化实现,对第i个训练样本(一个nx的向量),与维度同为nx的dz向量相乘。
向量化的逻辑回归
非向量化实现

向量化实现:
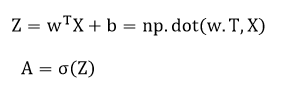
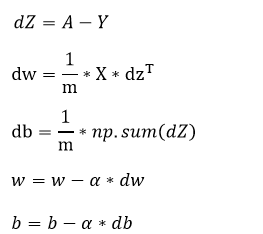
在这里w是一个向量,x是一个向量,b是一个数