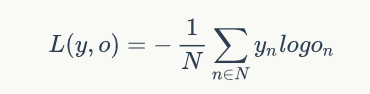最近准备文本的关系抽取,其中用到了LSTM和CRF,这里先贴出对循环神经网络的总结。
===========================================================
说明:本篇总结大部分是借鉴其他人的资料,在别人基础上补充了自己对RNN的理解。其实数学推导的话仔细看是不难的,除了在证明权重W、U的梯度是各个时刻权重梯度的和稍微有点麻烦,其他相信大家都能看懂
哈哈哈,总结下来感悟还是蛮深的,对RNN的理解又上了一层!!!!!!!!!
===========================================================
- 传统神经网络缺点
传统神经网络只能处理一个个的输入,前一个输入和后一个输入是完全没有关系的。对于卷积神经网络,虽然可以考虑到上下几个词的信息(这个依赖于你filter的大小)。但是如果想处理序列信息,即前面的输入和后面的输入都是有联系的,这就会用到循环神经网络。理论上,循环神经网络可以往前看任意多个词语。
- 语言模型
我昨天上学迟到了,老师批评了____。
我们给电脑展示了这句话前面这些词,然后,让电脑写下接下来的一个词。在这个例子中,接下来的这个词最有可能是『我』,而不太可能是『小明』,甚至是『吃饭』。
语言模型:给定一句话的前面部分,预测接下来最有可能的一个词是什么。
其实,在之前,N-Gram模型也可以作为语言模型。但是如果N非常大,模型的大小与N是成指数级的,会占用海量的存储空间。一般对于我们而言N=3已经是极限情况,N-gram无法向前看更多的词语。
- 循环神经网络结构
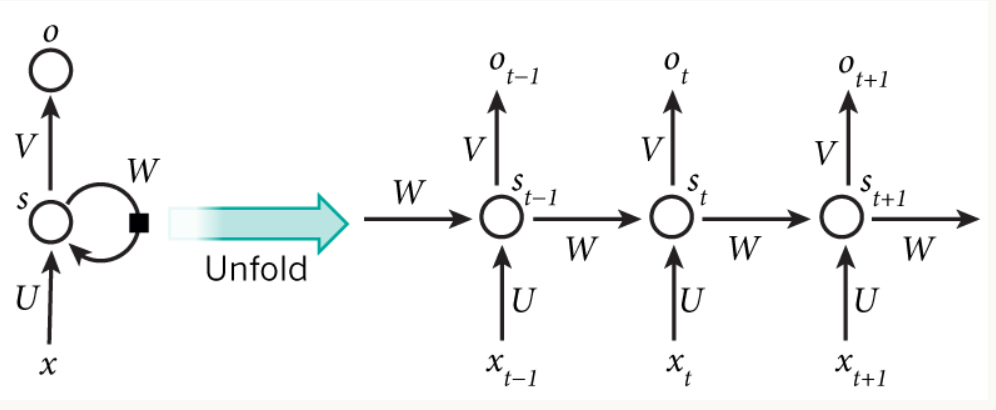
这里面没有画出来表示神经元节点的圆圈
隐藏层其实是多个节点,节点数与向量s的维度相同
在t时刻接受输入$$x_{t}$$之后,隐藏层的之位$$s_{t}$$,输出值是$$o_{t}$$。$$s_{t}$$的值不仅取决于$$x_{t}$$,还取决于$$s_{t
- 1}$$
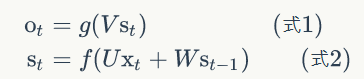
U是输入x的权重矩阵,W是上一次的值$$s_{t -
1}$$作为这一次的输入的权重矩阵,f是激活函数。
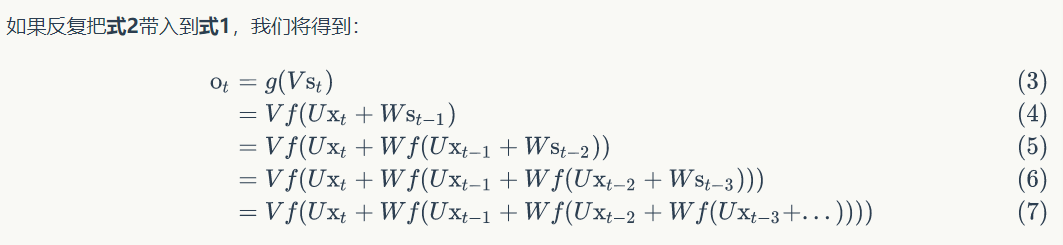
所以循环神经网络的输出$$o_{t}$$是受前面历次输入值$$x_{t}$$,$$x_{t -
1}$$,$$x_{t -
2}$$….影响的,这就是为什么循环神经网络可以往前看任意多个输入值。
- 双向循环神经网络
例子:我的手机坏了,我打算____一部新手机。
手机坏了,那么我是打算修一修?换一部新的?还是大哭一场?这些都是无法确定的。但如果我们也看到了横线后面的词是『一部新手机』,那么,横线上的词填『买』的概率就大得多了。
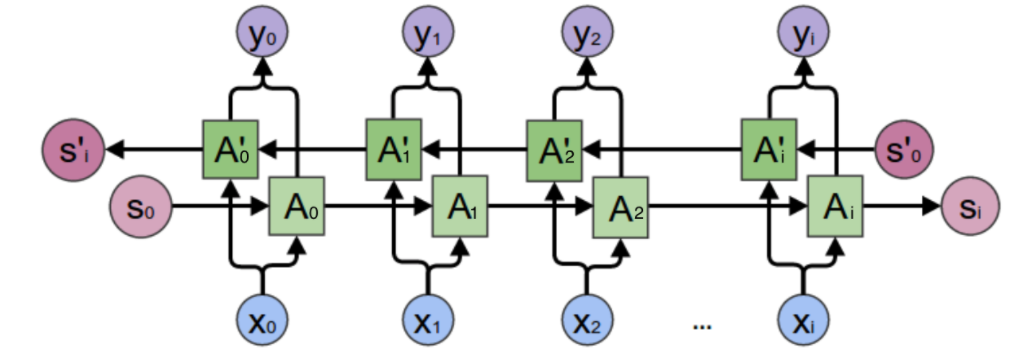
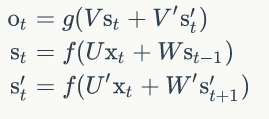
正向计算和反向计算不共享权重,也就是说U和U’、W和W’、V和V’都是不同的权重矩阵。
- 深度循环神经网络
前面我们介绍的循环神经网络只有一个隐藏层,我们当然也可以堆叠两个以上的隐藏层,这样就得到了深度循环神经网络。如下图所示:
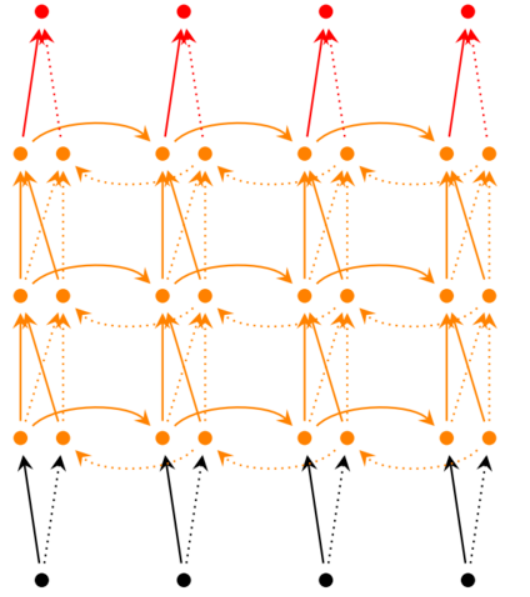

对于隐藏层第i层,矩阵U乘的是t时刻前一层i-1层的值st(i-1)
,W乘的是t-1时刻第l层的值st-1(i)(这里我感觉上面没写清楚)
- 循环神经网络的训练BPTT算法
思路:误差传递分两块,其一是沿着时间线的反向传递用于更新权重矩阵W,其一是沿着层数的反向传递用于更新权重矩阵U。
前向计算每个神经元的输出值;
反向计算每个神经元的误差项值,它是误差函数E对神经元j的加权输入的偏导数;
计算每个权重的梯度。
最后再用随机梯度下降算法更新权重。这里的误差函数,对于循环神经网络而言,一般选择交叉熵损失函数
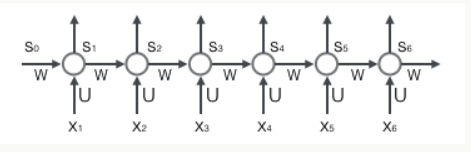
6.1 前向计算
我们假设输入向量x的维度是m,输出向量s的维度是n,则矩阵U的维度是,矩阵W的维度是。下面是上式展开成矩阵的样子,看起来更直观一些:
自己理解:输入向量x的维度为m,那么输入层就有m个神经元,每个神经元接受输入向量x的一个维度的值。向量s的维度为n,那么隐藏层就有n个神经元。这些具体的神经元在上图中都没有画出来,它只是抽象的网络在时间上进行展开了而已(一个圆圈代表了很多个神经元节点)。
重要的事情说三遍!!!!!!!!!!!!!!
上面的圆圈代表的不是一个神经元
上面的圆圈代表的不是一个神经元
上面的圆圈代表的不是一个神经元

Sjt表示向量s的第j个元素在t时刻的值(隐层第j个神经元在t时刻的值)
uji表示输入层第i个神经元到循环层第j个神经元的权重
Wji表示循环层第t-1时刻的第i个神经元到循环层第t个时刻的第j个神经元的权重(不要嫌我啰嗦,这里再说一下,上面的一个圈代表的是某时刻一组神经元)。
6.2 后向传播
神经元j的误差项定义:交叉熵损失函数对神经元j的加权输入的偏导数;

沿时间线反向传递
某神经元在k时刻的误差项为(其中netk为该神经元的加权输入):

如何计算上式:
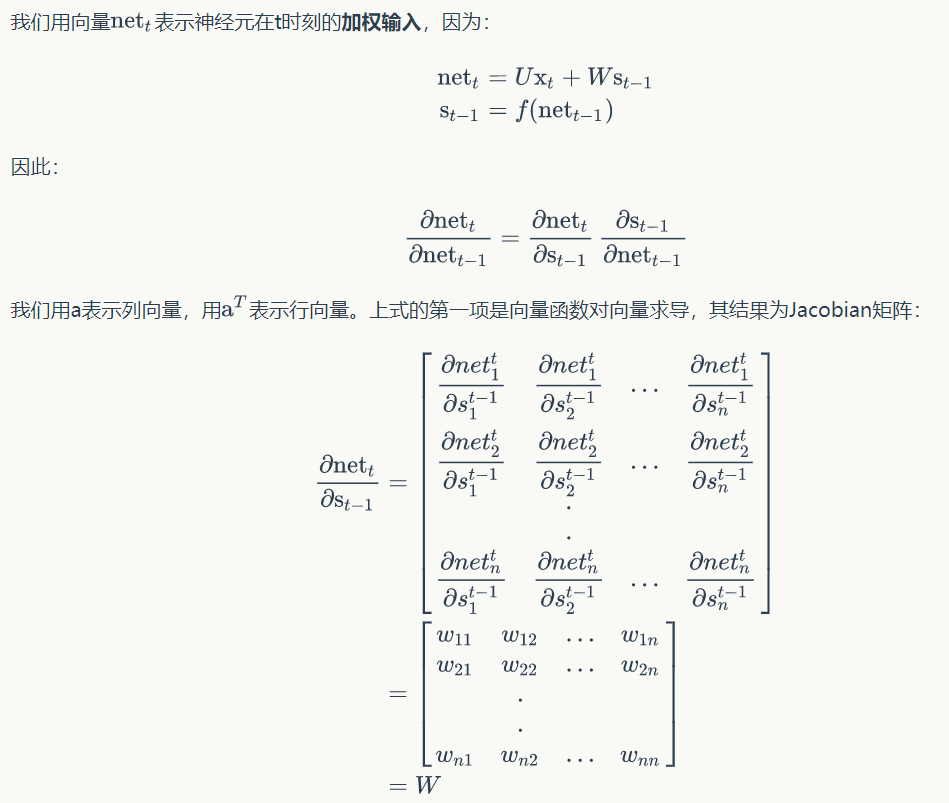
这里建议大家看一下向量函数对向量求导的知识,求一阶导数得到Jacobian矩阵,二阶导得到Heissan矩阵
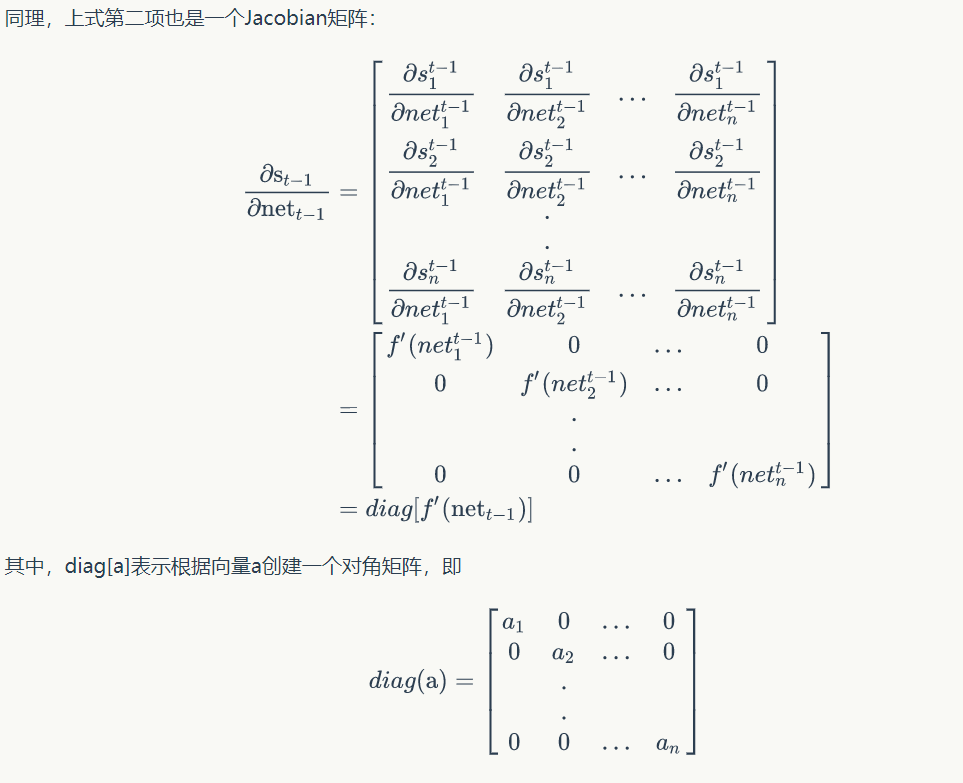
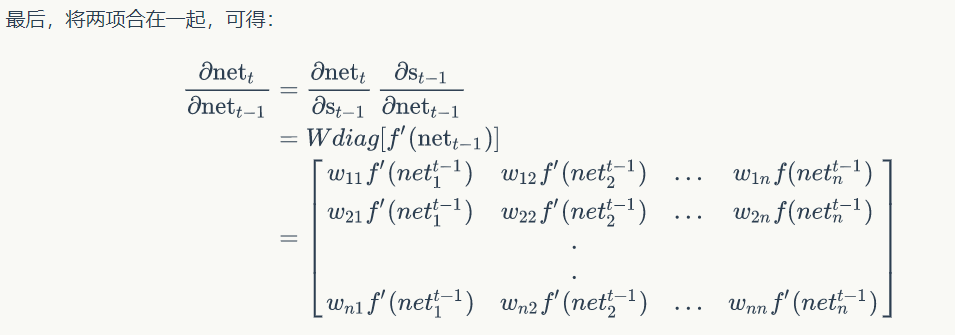
带入误差项定义式子得到:

沿网络层数反向传递

由上面式子可以得到:
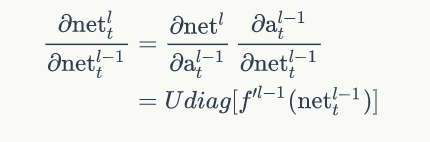
第l-1层某神经元在t时刻的误差项定义为损失函数对该神经元加权输入的偏导:
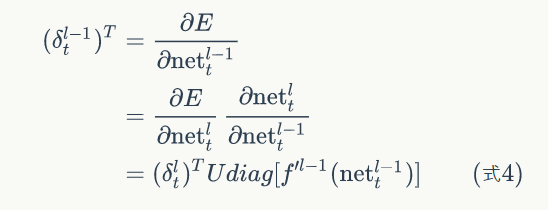
6.3 权重更新:用梯度下降法,更新公式如下所示
权重:=权重 - 学习率*损失函数对权重的梯度
所以先计算权重梯度:以计算损失函数对权重矩阵W为例讲解
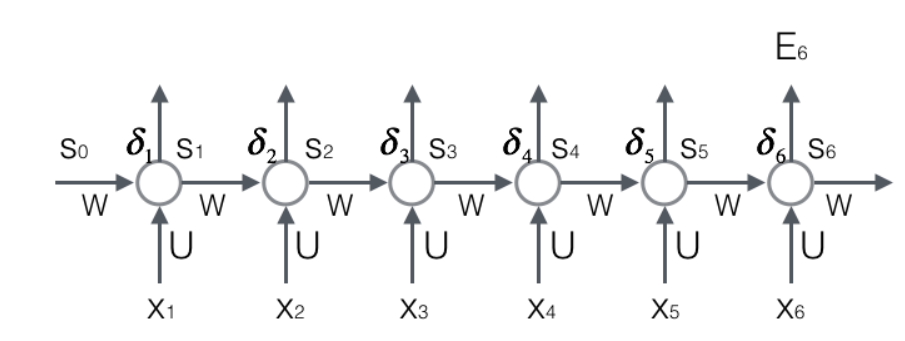
普通神经网络的权重梯度算法:只要知道任意层的神经元误差项以及上一层的输出激活值a,就可以求出权重矩阵在l任意层的梯度。迁移到循环神经网络:只要知道了任意一个时刻的误差项,以及上一个时刻循环层的输出值,即可求出权重矩阵t时刻的梯度。
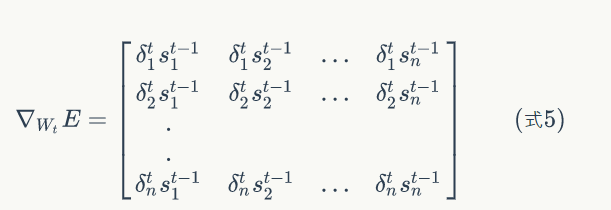
推导如下所示:


具体证明过程这里不解释,可参考https://zybuluo.com/hanbingtao/note/541458

- 梯度消失与梯度爆炸问题
问题:前面介绍的几种RNN不能很好的处理较长的序列。主要原因在于RNN在训练中容易发生梯度消失与梯度爆炸的问题,使得RNN无法捕捉到长距离的影响。(但是现在有LSTM完美的解决了上述的问题)
根据误差项的反向传播(沿着时间轴反向传播):
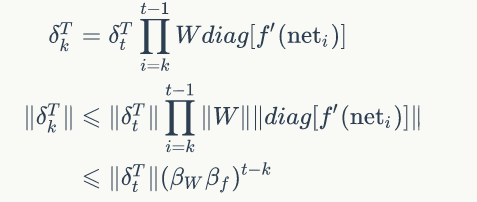
如果t-k很大的话(也就是向前看很远的时候),会导致对应的误差项的值增长或缩小的非常快,这样就会导致相应的梯度爆炸和梯度消失问题。取决于β大于1还是小于1
总结:梯度消失于梯度爆炸表现在沿着时间轴线反向传播上,不能往前看很长的序列。另一方面,如果我们用的RNN很深,层数很大,也会造成梯度消失与梯度爆炸的问题。
- RNN应用举例:
我们首先把词依次输入到循环神经网络中,每输入一个词,循环神经网络就输出截止到目前为止,下一个最可能的词。例如,当我们依次输入
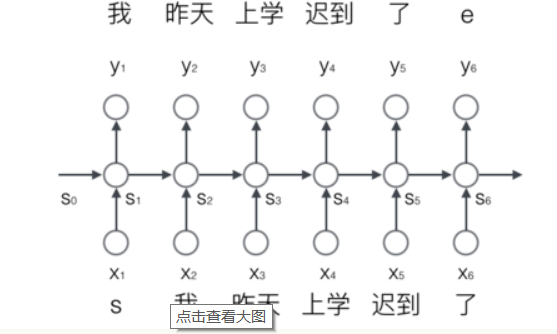
解释内部运行机理:
首先先明确,每个圆圈指的不是一个神经元,而是一层的神经元。在输入“我”的时候,先把“我”转成embedding向量(假设维度为m),那么圆圈x2就有m个神经元接受这个向量,并乘以矩阵U(m*n)得到n维度向量(n为隐层s的向量维度或者叫做隐层神经元的数量)。那么如何计算s2呢?假设隐层s的值为n维向量(隐层有n个神经元,每个神经元输出n维向量某一维度的值),这个n维向量乘以矩阵W(n*n)变为n为向量。将两个n维度向量相加得到n维度向量,s2代表的一组n个神经元接受该n维向量,每个神经元接受一个维度的值,并用激活函数激活,然后输出。
语言模型要求的输出是下一个最可能的词,我们可以让循环神经网络计算计算词典中每个词是下一个词的概率,这样,概率最大的词就是下一个最可能的词。因此,神经网络的输出向量也是一个N维向量,向量中的每个元素对应着词典中相应的词是下一个词的概率。如下图所示:
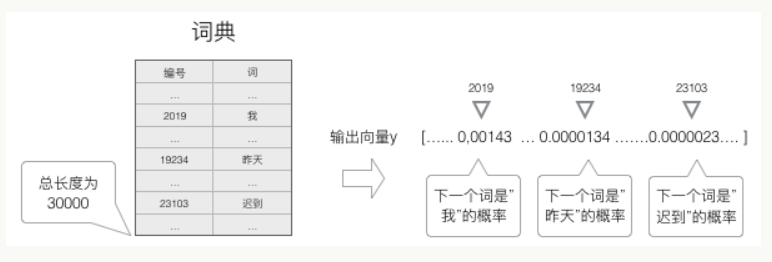
那么,怎么样才能让神经网络输出概率呢?方法就是用softmax层作为神经网络的输出层。
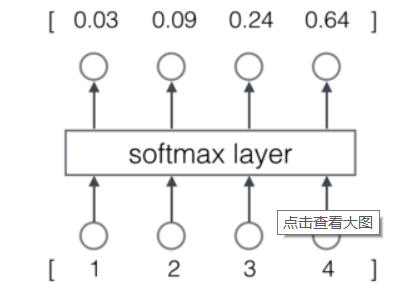

- 交叉熵误差
当神经网络的输出层是softmax层时,对应的误差函数E通常选择交叉熵误差函数